Объекты показанные на рисунке удовлетворяют отношению встав( Дер 6 НДа Мб НДб)
Рисунок 10. 4. Объекты, показанные на рисунке, удовлетворяют отношению встав( Дер, 6, НДа, Мб, НДб).
2-3 деревья мы будем представлять в программе следующим образом:
- nil представляет пустое дерево;
- л( Х) представляет дерево, состоящее из одной вершины - листа с элементом X;
- в2( Д1, М, Д2) представляет дерево с двумя поддеревьями Д1 и Д2; М - минимальный элемент из Д2;
- в3( Д1, М2, Д2, М3, Д3) представляет дерево с тремя поддеревьями Д1, Д2 и Д3; М2 - минимальный элемент из Д2; М3 - минимальный элемент из Д3; Д1, Д2 и Д3 - 2-3 деревья.
Между доб23 и встав существует следующая связь: если после вставления нового элемента дерево не "вырастает", то
доб23( Дер, X, НовДер) :-
встав( Дер, X, НовДер).
Однако если после вставления элемента глубина дерева увеличивается, то встав порождает два поддерева Д1 и Д2, а затем составляет из них дерево большей глубины:
доб23( Дер, X, в2( Д1, М, Д2) ) :-
встав( Дер, X, Д1, М, Д2).
Отношение встав устроено более сложным образом, поскольку ему приходится иметь дело со многими случаями, а именно вставление в пустое дерево, в дерево, состоящее из одного листа, и в деревья типов в2 и в3. Возникают также дополнительные подслучаи, так как новый элемент можно вставить в первое, либо во второе, либо в третье поддерево. В связи с этим мы определим встав как набор правил таким образом, чтобы каждое предложение процедуры встав имело дело с одним из этих случаев. На Рисунок 10.5 показаны некоторые из возможных случаев. На Пролог они транслируются следующим образом:
Случай а
встав( в2( Д1, М, Д2), X, в2( НД1, М, Д2) ) :-
больше( М, X),
% М больше, чем Х
встав( Д1, X, НД1).
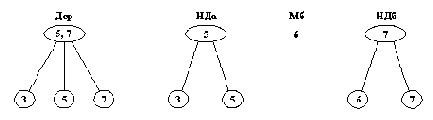
Случай b
встав( в2( Д1, M, Д2), X, в3( НД1а, Мб, НД1б, M, Д2) ) :-
больше( М, X),
встав( Д1, X, НД1а, Мб, НД1б).
Случай с
встав( в3( Д1, М2, Д2, М3, Д3), X, в2( НД1а, Мб, НД1б), М2, в2(Д2, М3, Д3) ) :-
больше( М2, X),
встав( Д1, X, НД1а, Мб, НД1б).