а) Пространство
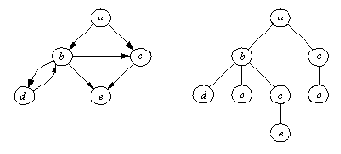
Рисунок 11. 14. (а) Пространство состояний; а - стартовая вершина.
(b) Дерево всех возможных ациклических путей, ведущих из а,
порожденное программой поиска в ширину.
длин - самые короткие решения идут первыми. Это является важным обстоятельством, если нам необходима оптимальность (в отношении длины решения). Стратегия поиска в ширину гарантирует получение кратчайшего решения первым. Разумеется, это неверно для поиска в глубину.
Наши программы, однако, не учитывают стоимости, приписанные дугам в пространстве состояний. Если критерием оптимальности является минимум стоимости решающего пути (а не его длина), то в этом случае поиска в ширину недостаточно. Поиск с предпочтением из гл. 12 будет направлен на оптимизацию стоимости.
Еще одна типичная проблема, связанная с задачей поиска, - это проблема комбинаторной сложности. Для нетривиальных предметных областей число альтернатив столь велико, что проблема сложности часто принимает критический характер. Легко понять, почему это происходит: если каждая вершина имеет b преемников, то число путей длины l, ведущих из стартовой вершины, равно bl ( в предположении, что циклов нет). Таким образом, вместе с увеличением длин путей наблюдается экспоненциальный рост объема множества путей-кандидатов, что приводит к ситуации, называемой комбинаторным взрывом. Стратегии поиска в глубину и ширину недостаточно "умны" для борьбы с такой степенью комбинаторной сложности: отсутствие селективности приводит к тому, что все пути рассматриваются как одинаково перспективные.
По-видимому, более изощренные процедуры поиска должны использовать какую-либо информацию, отражающую специфику данной задачи, с тем чтобы на каждой стадии поиска принимать решения о наиболее перспективных путях поиска. В результате процесс будет продвигаться к целевой вершине, обходя бесполезные пути. Информация, относящаяся к конкретной решаемой задаче и используемая для управления поиском, называется эвристикой. Про алгоритмы, использующие эвристики, говорят, что они руководствуются эвристиками: они выполняют эвристический поиск. Один из таких методов изложен в следующей главе.