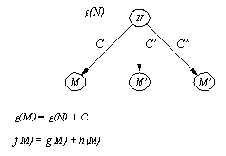
Связь между gоценкой
Рисунок 12. 5. Связь между g-оценкой вершины В и f- и g-оценками
ее "детей" в пространстве состояний.
line();
Алгоритм поиска пути называют допустимым, если он всегда отыскивает оптимальное решение (т.е. путь минимальной стоимости) при условии, что такой путь существует. Наша реализация алгоритма поиска, пользуясь механизмом возвратов, выдает все существующие решения, поэтому, в нашем случае, условием допустимости следует считать оптимальность первого из найденных решений. Обозначим через h*(n) стоимость оптимального пути из произвольной вершины n в целевую вершину. Верна следующая теорема о допустимости А*-алгоритма: А*-алгоритм, использующий эвристическую функцию h, является допустимым, если
h( n) <= h*( n)
для всех вершин n пространства состояний.
line();Этот результат имеет огромное практическое значение. Даже если нам не известно точное значение h*, нам достаточно найти какую-либо нижнюю грань h* и использовать ее в качестве h в А*-алгоритме - оптимальность решения будет гарантирована.
Существует тривиальная нижняя грань, а именно:
h( n) = 0, для всех вершин n пространства состояний.
И при таком значении h допустимость гарантирована. Однако такая оценка не имеет никакой эвристической силы и ничем не помогает поиску. А*-алгоритм при h=0 ведет себя аналогично поиску в ширину. Он, действительно, превращается в поиск в ширину, если, кроме того, положить с(n, n' )=1 для всех дуг (n, n') пространства состояний. Отсутствие эвристической силы оценки приводит к большой комбинаторной сложности алгоритма. Поэтому хотелось бы иметь такую оценку h, которая была бы нижней гранью h* (чтобы обеспечить допустимость) и, кроме того, была бы как можно ближе к h* (чтобы обеспечить эффективность). В идеальном случае, если бы нам была известна сама точная оценка h*, мы бы ее и использовали: А*-алгоритм, пользующийся h*, находит оптимальное решение сразу, без единого возврата.