Три стартовых позиции
Рисунок 12. 7. Три стартовых позиции для "игры в восемь": (а) решение требует
4 шага; (b) решение требует 5 шагов; (с) решение требует 18 шагов.
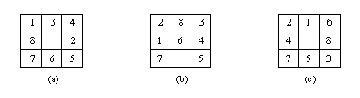
Наша задача - минимизировать длину решения, поэтому мы положим стоимости всех дуг пространства состояний равными 1. В программе Рисунок 12. 6. даны также определения трех начальных позиций (см. Рисунок 12.7).
Эвристическая функция h, запрограммирована как отношение
h( Поз, Н)
Поз - позиция на доске; Н вычисляется как комбинация из двух оценок:
(1) сумрасст - "суммарное расстояние" восьми фишек, находящихся в позиции Поз, от их положений в целевой позиции. Например, для начальной позиции, показанной на Рисунок 12.7(а), сумрасст = 4.
(2) упоряд - степень упорядоченности фишек в текущей позиции по отношению к тому порядку, в котором они должны находиться в целевой позиции. Величина упоряд вычисляется как сумма очков, приписываемых фишкам, согласно следующим правилам:
- фишка в центральной позиции - 1 очко;
- фишка не в центральной позиции, и непосредственно за ней следует (по часовой стрелке) та фишка, какая и должна за ней следовать в целевой позиции - 0 очков.
- то же самое, но за фишкой следует "не та" фишка - 2 очка.
Например, для начальной позиции Рисунок 12.7(а),
упоряд = 6.
Эвристическая оценка Н вычисляется как сумма
Н = сумрасст + 3 * упоряд
Эта эвристическая функция хорошо работает в том смысле, что она весьма эффективно направляет поиск к цели. Например, при решении головоломок Рисунок 12.7(а) и (b) первое решение обнаруживается без единого отклонения от кратчайшего решающего пути. Другими словами, кратчайшие решения обнаруживаются сразу, без возвратов. Даже трудная головоломка Рисунок 12.7 (с) решается почти без возвратов. Но данная эвристическая функция страдает тем недостатком, что она не является допустимой: нет гарантии, что более короткие пути обнаруживаются раньше более длинных. Дело в том, что для функции h условие h <= h* выполнено не для всех вершин пространства состояний. Например, для начальной позиции Рисунок 12.7 (а)
h = 4 + 3 * 6 = 22, h* = 4
С другой стороны, оценка "суммарное расстояние" допустима: для всех позиций
сумрасст <= h*
Доказать это неравенство можно при помощи следующего рассуждения: если мы ослабим условия задачи и разрешим фишкам взбираться друг на друга, то каждая фишка сможет добраться до своего целевого положения по траектории, длина которой в точности равна манхеттеновскому расстоянию между ее начальным и целевым положениями. Таким образом, длина оптимального решения упрощенной задачи будет в точности равна сумрасст. Однако в исходном варианте задачи фишки взаимодействуют друг с другом и мешают друг другу, так что им уже трудно идти по своим кратчайшим траекториям. В результате длина оптимального решения окажется больше либо равной сумрасст.