а) Решить Р это
Рисунок 13. 3. (а) Решить Р - это значит решить Р1 или Р2 или ...
(б) Решить Q - это значит решить все: Q1 и Q2 и ... .
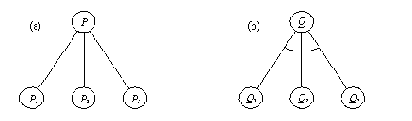
Итак, мы имеем две главных альтернативы для решения исходной задачи: (1) путь через f или (2) путь через g. Далее, каждую из этих альтернатив можно разбить на подзадачи (1.1 и 1.2 или 2.1 и 2.2 соответственно). Здесь важно то обстоятельство, что каждую из подзадач в обоих альтернативах можно решать независимо от другой. Полученное разбиение исходной задачи можно изобразить в форме И / ИЛИ-графа (Рисунок 13.2). Обратите внимание на полукруглые дуги, которые указывают на отношение И между соответствующими подзадачами. Граф, показанный на Рисунок 13.2 - это всего лишь верхняя часть всего И / ИЛИ-дерева. Дальнейшее разбиение подзадач можно было бы строить на основе введения дополнительных промежуточных городов.
Какие вершины И / ИЛИ-графа являются целевыми? Целевые вершины - это тривиальные, или "примитивные" задачи. В нашем примере такой подзадачей можно было бы считать подзадачу "найти путь из а в с", поскольку между городами а и с на карте имеется непосредственная связь.
Рассматривая наш пример, мы ввели ряд важных понятий. И / ИЛИ-граф - это направленный граф, вершины которого соответствуют задачам, а дуги - отношениям между задачами. Между дугами также существуют свои отношения. Это отношения И и ИЛИ, в зависимости от того, должны ли мы решить только одну из задач-преемников или же несколко из них (см. Рисунок 13.3). В принципе из вершины могут выходить дуги, находящиеся в отношении И вместе с дугами, находящимися в отношении ИЛИ. Тем не менее, мы будем предполагать, что каждая вершина имеет либо только И-преемников, либо только ИЛИ-преемников; дело в том, что в такую форму можно преобразовать любой И / ИЛИ граф, вводя в него при необходимости вспомогательные ИЛИ-вершины. Вершину, из которой выходят только И-дуги, называют И-вершиной; вершину, из которой выходят только ИЛИ-дуги, - ИЛИ-вершиной.
Когда задача представлялась в форме пространства состояний, ее решением был путь в этом пространстве. Что является решением в случае И / ИЛИ-представления? Решение должно, конечно, включать в себя все подзадачи И-вершины. Следовательно, это уже не путь, а дерево. Такое решающее дерево Т определяется следующим образом:
- исходная задача Р - это корень дерева Т;
- если Р является ИЛИ-вершиной, то в Т содержится только один из ее преемников (из И / ИЛИ-графа) вместе со своим собственным решающим деревом;
- если Р - это И-вершина, то все ее преемники (из И / ИЛИ-графа) вместе со своими решающими деревьями содержатся в Т.