Игры двух лиц с полной информацией
Игры, которые мы собираемся обсуждать в данной главе, относятся к классу так называемых игр двух лиц с полной информацией. Примерами таких игр могут служить шахматы, шашки и т.п. В игре участвуют два игрока, которые ходят по очереди, причем оба они обладают полной информацией о текущей игровой ситуации (это определение исключает большинство карточных игр). Игра считается оконченной, если достигнута позиция, являющаяся согласно правилам игры "терминальной" (конечной), например матовая позиция в шахматах. Правилами игры также устанавливается, каков исход игры в этой терминальной позиции.
Для игр такого рода возможно представление в виде дерева игры (или игрового дерева). Вершины этого дерева соответствуют ситуациям, а дуги ходам. Начальная ситуация игры - это корневая вершина; листьями дерева представлены терминальные позиции.
В большинстве игр этого типа возможны следующие исходы: выигрыш, проигрыш и ничья. Мы будем рассматривать здесь игры, имеющие только два возможных исхода - выигрыш и проигрыш. Игры, в которых возможна ничья, можно упрощенно считать играми с двумя исходами - выигрыш и не-выигрыш. Двух участников игры мы будем называть "игроком" и "противником". "Игрок" может выиграть в некоторой нетерминальной позиции с ходом игрока ("позиции игрока"), если в ней существует какой-нибудь разрешенный ход, приводящий к выигрышу. С другой стороны, некоторая нетерминальная позиция с ходом противника ("позиция противника") является выигранной для игрока, если все разрешенные ходы из этой позиции ведут к позициям, в которых возможен выигрыш. Эти правила находятся в полном соответствии с представлением задач в форме И / ИЛИ-дерева, которое мы обсуждали в гл. 13.Между понятиями, относящимися к И / ИЛИ-деревьям, и понятиями, используемыми в играх, можно установить взаимное соответствие следующим образом:
позиции игры вершины, задачи
терминальные позиции целевые вершины,
выигрыша тривиально решаемые задачи
терминальные позиции задачи, не имеющие решения
проигрыша
выигранные позиции задачи, имеющие решение
позиции игрока ИЛИ-вершины
позиции противника И-вершины
Очевидно, что аналогичным образом понятия, относящиеся к поиску в И / ИЛИ-деревьях, можно переосмыслить в терминах поиска в игровых деревьях.
Ниже приводится простая программа, которая определяет, является ли некоторая позиция игрока выигранной.
выигр( Поз) :-
терм_выигр( Поз).
% Терминальная выигранная позиция
выигр( Поз) :-
not терм_проигр( Поз),
ход( Поз, Поз1), % Разрешенный ход в Поз1
not ( ход( Поз1, Поз2),
not выигр( Поз2) ).
% Ни один из ходов противника не ведет к не-выигрышу
Здесь правила игры встроены в предикат ход( Поз, Поз1), который порождает все разрешенные ходы, а также в предикаты терм_выигр( Поз) и терм_проигр( Поз), которые распознают терминальные позиции, являющиеся, согласно правилам игры, выигранными или проигранными. В последнем из правил программы, содержащем двойное отрицание (not), говорится: не существует хода противника, ведущего к не выигранной позиции. Другими словами: все ходы противника приводят к позициям, выигранным с точки зрения игрока.
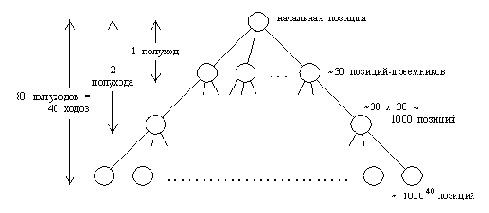
Рис. 15. 1. Сложность игровых деревьев в шахматах. Оценки основаны
на том, что в каждой шахматной позиции существуют приблизительно
30 разрешенных ходов я что терминальные позиции расположены на
глубине 40 ходов. Один ход равен двум полуходам (по одному
полуходу с каждой стороны).
Так же, как и аналогичная программа поиска в И / ИЛИ-графах, приведенная выше программа использует стратегию в глубину. Кроме того, в ней не исключается возможность зацикливания на одних и тех же позициях. Попытка устранить этот недостаток может привести к осложнениям, поскольку правила некоторых из игр допускают такое повторение позиций. Правда, разрешение повторять позиции часто носит условный характер, например по шахматным правилам после троекратного повторения позиции может быть объявлена ничья.
Программа, которую мы составили, демонстрирует основные принципы программирования игр. Но практически приемлемая реализация таких сложных игр, как шахматы или го, потребовала бы привлечения значительно более мощных методов. Огромная комбинаторная сложность этих игр делает наш наивный переборный алгоритм, просматривающий дерево вплоть до терминальных игровых позиций, абсолютно непригодным. Этот вывод иллюстрирует (на примере шахмат) рис. 15.1: пространство поиска имеет астрономические размеры - около 10120 позиций. Можно возразить, что в дереве на рис. 15.1 встречаются одинаковые позиции. Однако было показано, что число различных позиций дерева поиска находится далеко за пределами возможностей вычислительных машин обозримого будущего.