обезьяна и банан
Задача об обезьяне и банане часто используется в качестве простого примера задачи из области искуственного интеллекта. Наша пролог-программа, способная ее решить, показывает, как механизмы сопоставления и автоматических возвратов могут применяться для подобных целей. Мы сначала составим программу, не принимая во внимание процедурную семантику, а затем детально изучим ее процедурное поведение. Программа будет компактной и наглядной.
Рассмотрим следующий вариант данной задачи. Возле двери комнаты стоит обезьяна. В середине этой комнаты к потолку подвешен банан. Обезьяна голодна и хочет съесть банан, однако она не может дотянуться до него, находясь на полу. Около окна этой же комнаты на полу лежит ящик, которым обезьяна может воспользоваться. Обезьяна может предпринимать следующие действия: ходить по полу, залезать на ящик, двигать ящик (если она уже находится около него) и схватить банан, если она стоит на ящике прямо под бананом. Может ли обезьяна добраться до банана?
Одна из важных проблем при программировании состоит в выборе (адекватного) представления решаемой задачи в терминах понятий используемого языка программирования. В нашем случае мы можем считать, что "обезьяний мир" всегда находится в некотором состоянии, и оно может изменяться со временем. Текущее состояние определяется взаиморасположением объектов. Например, исходное состояние мира определяется так:
(1) Обезьяна у двери.
(2) Обезьяна на полу.
(3) Ящик у окна.
(4) Обезьяна не имеет банана.
Удобно объединить все эти четыре информационных фрагмента в один структурный объект. Давайте в качестве такого объединяющего функтора выберем слово "состояние". На рис. 2.12 в виде структурного объекта изображено исходное состояние.
Нашу задачу можно рассматривать как игру для одного игрока. Давайте, формализуем правила этой игры.
Первое, целью игры является ситуация, в которой обезьяна имеет банан, т. е. любое состояние, у которого в качестве четвертой компоненты стоит "имеет":
состояние( -, -, -, имеет)
Второе, каковы разрешенные ходы, переводящие мир из одного состояния в другое? Существуют четыре типа ходов:
(1) схватить банан,
(2) залезть на ящик,
(3) подвинуть ящик,
(4) перейти в другое место.
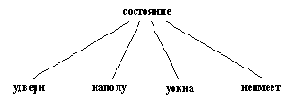
Рис. 2. 12. Исходное состояние обезьяньего мира, представленное в виде структурного объекта. Его четыре компоненты суть горизонтальная позиция обезьяны, вертикальная позиция обезьяны, позиция ящика, наличие или отсутствие у обезьяны банана.
Не всякий ход допустим при всех возможных состояниях мира. Например, ход "схватить" допустим, только если обезьяна стоит на ящике прямо под бананом (т.е. в середине комнаты) и еще не имеет банана. Эти правила можно формализовать в Прологе в виде трехместного отношения ход:
ход( Состояние1, М, Состояние2)
Три аргумента этого отношения определяют ход, следующим образом:
Состояние1 --------> Состояние2
М
Состояние1 это состояние до хода, М - выполняемый ход, и Состояние2 - состояние после хода.
Ход "схватить", вместе с необходимыми ограничениями на состояние перед этим ходом, можно выразить такой формулой:
ход( состояние( середина, наящике, середина, неимеет),
% Перед ходом
схватить, % Ход
состояние( середина, наящике, середина, имеет) ).
% После хода
В этом факте говорится о том, что после хода у обезьяны уже есть банан и что она осталась на ящике в середине комнаты.
Таким же способом можно выразить и тот факт, что обезьяна, находясь на полу, может перейти из любой горизонтальной позиции Р1 в любую позицию Р2. Обезьяна может это сделать независимо от позиции ящика, а также независимо от того, есть у нее банан или нет. Все это можно записать в виде следующего прологовского факта:
ход( состояние( Р1, наполу, В, Н),
перейти( Р1, Р2), % Перейти из Р1 в Р2
состояние( Р2, наполу, В, Н) ).
Заметим, что в этом предложении делается много утверждений и, в частности:
- выполненный ход состоял в том, чтобы "перейти из некоторой позиции Р1 в некоторую позицию Р2";
- обезьяна находится на полу, как до, так и после хода;
- ящик находится в некоторой точке В, которая осталась неизменной после хода;
- состояние "имеет банан" остается неизменным после хода.
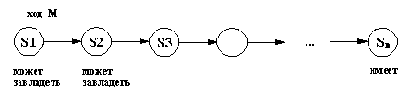
Рис. 2. 13. Рекурсивная формулировка отношения можетзавладетъ.
Данное предложение на самом деле определяет все множество возможных ходов указанного типа, так как оно применимо к любой ситуации, сопоставимой с состоянием, имеющим место перед входом.
Поэтому такое предложение иногда называют схемой хода. Благодаря понятию переменной, имеющемуся в Прологе, такие схемы легко на нем запрограммировать.
Два других типа ходов: "подвинуть" и "залезть" - легко определить аналогичным способом.
Главный вопрос, на который должна ответить наша программа, это вопрос: "Может ли обезьяна, находясь в некотором начальном состоянии S, завладеть бананом?" Его можно сформулировать в виде предиката
можетзавладеть( S)
где аргумент S - состояние обезьяньего мира. Программа для можетзавладеть может основываться на двух наблюдениях:
(1) Для любого состояния S, в которой обезьяна уже имеет банан, предикат можетзавладеть должен, конечно, быть истинным; в этом случае никаких ходов не требуется. Вот соответствующий прологовский факт:
можетзавладеть( состояние( -, -, -, имеет) ).
(2) В остальных случаях требуется один или более ходов. Обезьяна может завладеть бананом в любом состоянии S1, если для него существует ход из состояния Р1 в некоторое состояние S2, такое, что, попав в него, обезьяна уже сможет завладеть бананом (за нуль или более ходов). Этот принцип показан на рис. 2.13. Прологовская формула, соответствующая этому правилу, такова:
можетзавладеть( S1) :-
ход( S1, М, S2),
можетзавладеть( S2).
Теперь мы полностью завершили нашу программу, показанную на рис. 2.14.
Формулировка можетзавладеть рекурсивна и совершенно аналогична формулировке отношения предок из гл. 1 (ср. рис. 2.13 и 1.7). Этот принцип используется в Прологе повсеместно.
Мы создали нашу программу "непроцедурным" способом. Давайте теперь изучим ее процедурное поведение, рассмотрев следующий вопрос к программе:
?- можетзавладеть( состояние( удвери, наполу, уокна, неимеет) ).
Ответом пролог-системы будет "да". Процесс, выполняемый ею при этом, обрабатывает, в соответствии с процедурной семантикой Пролога, последовательность списков целей. Для этого требуется некоторый перебор ходов, для отыскания верного из нескольких альтернативных. В некоторых точках при таком переборе будет сделан неверный ход, ведущий в тупиковую ветвь процесса вычислений. На этом этапе автоматический возврат позволит исправить положение. На рис. 2.15 изображен процесс перебора.
line(); % Разрешенные ходы
ход( состояние( середина, на ящике, середина, неимеет),
схватить, % Схватить банан
состояние( середина, наящике, середина, имеет)).
ход( состояние( Р, наполу, Р, Н),
залезть, % Залезть на ящик
состояние( Р, наящике, Р, Н) ).
ход( состояние( Р1, наполу, Р1, Н),
подвинуть( Р1, Р2), % Подвинуть ящик с Р1 на Р2
состояние( Р2, наполу, Р2, Н) ).
ход( состояние( Р1, наполу, В, Н),
перейти( Р1, Р2), % Перейти с Р1 на Р2
состояние( Р2, наполу, В, Н) ).
% можетзавладеть(Состояние): обезьяна может завладеть
% бананом, находясь в состоянии Состояние
можетзавладеть( состояние( -, -, -, имеет) ).
% может 1: обезьяна уже его имеет
можетзавладеть( Состояние1) :-
% может 2: Сделать что-нибудь, чтобы завладеть им
ход( Состояние1, Ход, Состояние2),
% сделать что-нибудь
можетзавладеть( Состояние2).
% теперь может завладеть
line(); Рис. 2. 14. Программа для задачи об обезьяне и банане.
Для ответа на наш вопрос системе пришлось сделать лишь один возврат. Верная последовательность ходов была найдена почти сразу. Причина такой эффективности программы кроется в том порядке, в
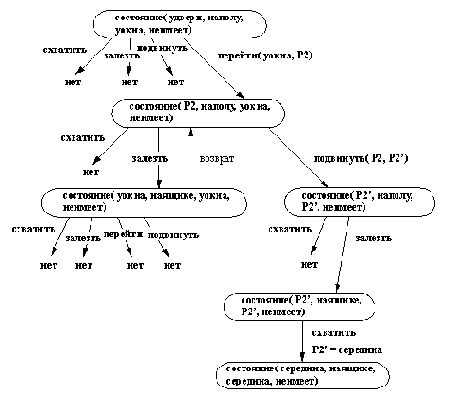
Рис. 2. 15. Поиск банана обезьяной. Перебор начинается в верхнем узле и распространяется вниз, как показано. Альтернативные ходы перебираются слева направо. Возврат произошел только один раз.
котором в ней расположены предложения, касающиеся отношения ход. В нашем случае этот порядок (к счастью) оказался весьма подходящим. Однако возможен и менее удачный порядок. По правилам игры обезьяна могла бы с легкостью ходить туда-сюда, даже не касаясь ящика, или бесцельно двигать ящик в разные стороны. Как будет видно из следующего раздела, более тщательное исследование обнаруживает, что порядок предложений в нашей программе является, на самом деле, критическим моментом для успешного решения задачи.
Назад | Содержание | Вперёд