Задача о ханойской башне
Задача о ханойской башне (рис. 13.6) - это еще один классический пример эффективного применения метода разбиения задачи на подзадачи и построения И / ИЛИ-графа. Для простоты мы рассмотрим упрощенную версию этой задачи, когда в ней участвует только три диска:
Имеется три колышка 1, 2 и 3 и три диска а, b и с (а - наименьший из них, а с - наибольший). Первоначально все диски находятся на колышке 1. Задача состоит в том, чтобы переложить все диски на колышек 3. На каждом шагу можно перекладывать только один диск, причем никогда нельзя помещать больший диск на меньший.
Эту задачу можно рассматривать как задачу достижения следующих трех целей:
(1) Диск а
- на колышек 3.
(2) Диск b
- на колышек 3.
(3) Диск с
- на колышек 3.
Беда в том, что эти цели не независимы. Например, можно сразу переложить диск а на колышек 3, и первая цель будет достигнута. Но тогда две другие цели станут недостижимыми (если только мы не отменим первое наше действие). К счастью, существует такой удобный порядок достижения этих целей, из которого можно легко вывести искомое решение.
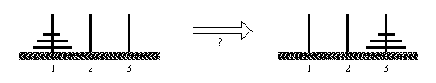
Рис. 13. 6. Задача о ханойской башне
Порядок этот можно установить при помощи следующего рассуждения: самая трудная цель - это цель 3 (диск с - на колышек 3), потому что на диск с наложено больше всего ограничений. В подобных ситуациях часто срабатывает хорошая идея: пытаться достичь первой самую трудную цель. Этот принцип основан на следующей логике: поскольку другие цели достигнуть легче (на них меньше ограничений), можно надеяться на то, что их достижение возможно без отмены действий на достижение самой трудной цели.
Применительно к нашей задаче это означает, что необходимо придерживаться следующей стратегии:
Первой достигнуть цель "диск с - на колышек 3",
а затем - все остальные.
Но первая цель не может быть достигнута сразу, так как в начальной ситуации диск с двигать нельзя. Следовательно, сначала мы должны подготовить этот ход, и наша стратегия принимает такой вид
(1) Обеспечить возможность перемещения диска с с 1 на 3.
(2) Переложить с с 1 на 3.
(3) Достигнуть остальные цели (а на 3 и b на 3).
Переложить c с 1 на 3 возможно только в том случае, если диск а и b оба надеты на колышек 2. Таким образом наша исходная задача перемещения а, b и с с 1 на 3 сводится к следующим трем подзадачам:
Для того, чтобы переложить a, b и с с 1 на 3, необходимо
(1) переложить а и b с 1 на 2, и
(2) переложить с с 1 на 3, и
(1) переложить а и b с 2 на 3.
Задача 2 тривиальна (она решается за один шаг). Остальные две подзадачи можно решать независимо от задачи 2, так как диски а и b можно двигать, не обращая внимание на положение диска с. Для решения задач 1 и 3 можно применить тот же самый принцип разбиения (на этот раз диск b будет самым "трудным"). В соответствии с этим принципом задача 1 сводится к трем тривиальным подзадачам:
Для того, чтобы переложить а и b с 1 на 2, необходимо:
(1) переложить а с 1 на 3, и
(2) переложить b с 1 на 2, и
(1) переложить а с 3 на 2.